Distances

Nous donnons ici la définition axiomatique des fonctions que l'on appelle 'distances', puis nous fournissons quelques exemples. C'est la donnée conjointe d'un ensemble et d'une distance sur cet ensemble qui définit un espace métrique.

Définitions

Soit E un ensemble. une distance sur E est une application d de E×E dans l'ensemble des nombres réels R, possédant les propriétés suivantes :

  • d(x,y)≥0 pour tout couple d'éléments (x,y) de E.
  • La relation d(x,y)=0 est équivalente à x=y.
  • d(x,y)=d(y,x) pour tout couple d'éléments de E.
  • d(x,z)≤d(x,y)+d(y,z) ∀ (x,y,z) ∈ E×E×E (inégalité dite du triangle)
Un espace métrique est la donnée conjointe d'un ensemble E et d'une distance d sur E. Un tel espace pourra être noté (E,d).
Deux distances distinctes d1 et d2 sur un même ensemble E définissent donc deux espaces métriques (E,d1) et (E,d2).

Propriété des distances

L'inégalité du triangle se généralise immédiatement par récurrence à n'importe quel polygone :

Si d est une distance sur E, et si x1, x2, ...,xn sont n points de E : d(x1,xn)≤n−1∑i=1d(xi,xi+1)

d(A,E)≤d(A,B)+d(B,C)+d(C,D)+d(D,E)

Si d est une distance sur E, alors :
|d(x,z)-d(y,z)|≤d(x,y)
En utilisant conjointement la symétrie d'une distance et l'inégalité du triangle on obtient : d(x,z) ≤ d(y,z)+d(x,y) d(y,z) ≤ d(y,x)+d(x,z)=d(x,y)+d(x,z) donc, -d(x,y)≤d(x,z)-d(y,z)≤d(x,y)

Exemples de distances

Exemple 1 (distance euclidienne sur R)

L'application (x,y) → d1(x,y)=|x-y| est une distance sur R

Exemple 2 (distance euclidienne sur R2)

Soient M(x,y) et M'(x',y') deux points de R2
d2(M,M′)=√(x−x′)2+(y−y′)2 est une distance sur R2

Exemple 3 (distance euclidienne sur R3)

Soient M(x,y,z) et M'(x',y',z') deux points de R3 d3(M,M′)=√(x−x′)2+(y−y′)2+(z−z′)2 est une distance sur R3

Exemple 4 (distance euclidienne sur Rn)

Soient M(x1,x2, ..., xn) et M'(x'1,x'2, ..., x'n) deux points de Rn
d4(M,M′)=√∑ni=1(xi−x′i)2 est une distance sur Rn c'est la généralisation des deux précédentes.

Exemple 5 (distance du sup sur Rn)

Soient M(x1,x2, ..., xn) et M'(x'1,x'2, ..., x'n) deux points de Rn d5(M,M′)=sup est une distance sur \mathbb{R}n

Exemple 6 (autre distance euclidienne sur \mathbb{R}n)

Soient M(x1,x2, ..., xn) et M'(x'1,x'2, ..., x'n) deux points de \mathbb{R}n d_{6}(M,M')=\sum_{i=1}^{n} |x_{i}-x'_{i}| est une distance sur \mathbb{R}n

Exemple 7

Soit K un ensemble quelconque et E l'ensemble des fonctions définies sur K, à valeurs réelles et bornées. E est donc en particulier un sous-espace vectoriel de \mathbb{R}K. d_{7}(f_{1},f_{2})=\sup _{k\in K}|f_{1}(k)-f_2(k)| est une distance sur E. l'exemple 5 en est un cas particulier quand K={1,2, ...,n}

Exemple 8 (Espace discret)

Soit E un ensemble quelconque. Posons d8(x,y)=1 si x≠y et d8(x,x)=0 ∀x∈ E. Alors d8 est une distance sur E. E muni de cette distance est dit espace métrique discret.

Une première extension, la distance d'un point à un sous-ensemble

La définition suivante résulte du fait qu'une distance prend ses valeurs dans \mathbb{R}+, que cet ensemble est borné inférieurement par 0 et donc que tout sous-ensemble de \mathbb{R}+ possède une borne inférieure.

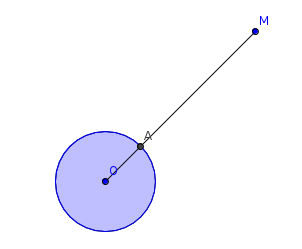
Soit (E,d) un espace métrique et F un sous-ensemble de E et x un élément de E. On pose d(x,F)=\inf_{y\in F}d(x,y) et d(x,F) s'appelle la distance de x à F, qui est donc un nombre ≥ 0.

Nous voyons tout de suite que si x ∈ F alors d(x,F)=0. Cependant la réciproque est fausse en effet si nous prenons le premier exemple, si x=0 et si F=]0,1[ nous avons bien d(x,F)=0 et x ∉ F. Le même contre-exemple peut servir à montrer que la distance de x à F peut ne pas être réalisée (ou atteinte) en un point y de F. En somme il est possible qu'il n'existe aucun point y de F tel que d(x,y)=d(x,F). Cependant il est également possible que la distance soit atteinte en un point et un seul comme ici où F est un cercle comportant sa circonférence et où x=M est un point externe à ce cercle.

Ou bien en deux ou même une infinité de points comme ici où x est le point M, centre d'un cercle et où F est l'extérieur de ce cercle au sens large incluant la circonférence:

 

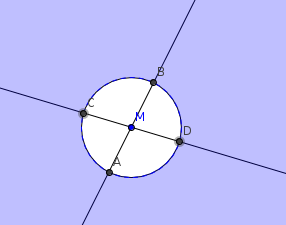
Une seconde extension, la distance de deux sous ensembles

Exactement comme dans le cas précédent, la définition suivante résulte du fait qu'une distance prend ses valeurs dans \mathbb{R}+, que cet ensemble est borné inférieurement par 0 et donc que tout sous-ensemble de \mathbb{R}+ possède une borne inférieure.

Soit (E,d) un espace métrique et F et K deux sous-ensembles de E. On pose d(F,K)=\inf_{x\in F, y\in K}d(x,y) et d(F,K) s'appelle la distance de F à K, qui est donc un nombre ≥ 0.

Si F\bigcap K\neq ∅ alors d(F,K)=0. la réciproque est fausse comme le montre l'exemple suivant où F={(x,y)| y>1/x et x >0} et K={(x,y) | y<-1/x et x>0}. La distance des deux ensembles est nulle mais ils n'ont aucun point commun.

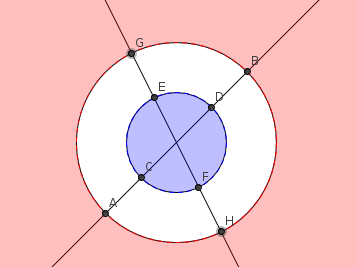
Il est possible cependant que la distance de F à K soit réalisée en un couple de points précisément, comme nous le voyons dans l'exemple suivant :

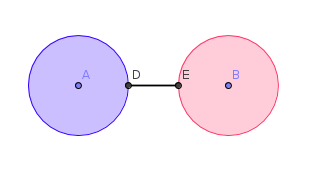
Mais il est possible également que la distance de F à K soit réalisée en une infinité de couples. Ici F est un disque et K l'extérieur d'un disque concentrique :

Exercices

Laisser un commentaire