Exercices sur les distances
d(x,y) ≤ Sup(d(x,z),d(z,y)) pour tout triplet (x,y,z) de points de E.
- Donner un exemple de distance ultramétrique.
- Pour toute distance ultramétrique, étant donné trois points, deux d'entre eux sont à la même distance du troisième, ce qui fait que tout triangle est isocèle
- Revoir les exemples du cours.
- Supposer par exemple que d(x,y)<d(y,z) et appliquer l'inégalité ultramétrique.
- L'exemple 08 (espace métrique discret) est un cas particulier d'espace ultramétrique.
-
Supposons par exemple que d(x,y)<d(y,z).
Puisque d(y,z) ≤ Sup(d(y,x),d(x,z)) on ne peut avoir aussi
d(x,z) < d(y,z)
Donc d(y,z) ≤ d(x,z)
Mais d(x,z) ≤ Sup(d(x,y),d(y,z))=d(y,z) par hypothèse.
et on a bien l'égalité.
Soit alors $x=_{-}^{+}\frac{r}{s}$ un nombre rationnel quelconque ≠ 0 posons vp(x)=vp(r)-vp(s).
Montrer que cette définition ne dépend pas de la représentation particulière de x par une fraction.
Posons maintenant pour tout couple de rationnels (x,y)
$d(x,y)=p^{-v_{p}(x-y)}$ si x ≠ y et d(x,x)=0.
Montrer que d est une distance sur l'ensemble $\mathbb{Q}$ des nombres rationnels. d s'appelle la distance p-adique.
En déduire que pour tout couple (x,y) de rationnels non nuls vp(xy)=vp(x)vp(y)
vp(x+y) ≥ Inf(vp(x),vp(y))
vp(x-y) ≥ Inf(vp(x),vp(y))
De là nous tirons :
d(x,y) ≤ Sup(d(x,z),d(y,z))
qui établit que d est une distance ultramétrique au sens de l'exercice précédent.
Exercices sur les isométries
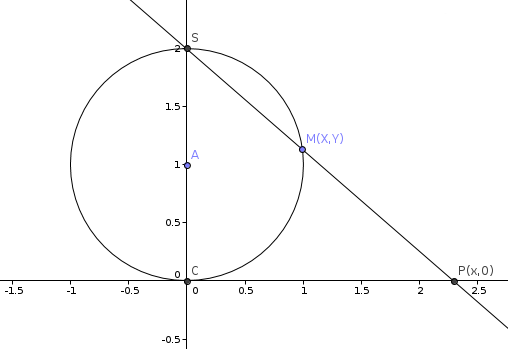
En vous inspirant de la construction de la droite réelle achevée. Montrer qu'on peut compléter la droite réelle aved un point de façon à ce obtenir un espace métrique isomorphe à un cercle (construction d'Alexandroff).
Exercices sur les boules
d(a,x) < r ⇒ d(x,y) ≤ Sup(d(x,a),d(a,y))< r ⇒ d(a',x) ≤ Sup(d(a',y),d(y,x)) < r'
Exercices sur les ouverts
Exercices sur les espaces topologiques
Le nombre total est donc 4.
$\bigcup_{i\in I}^{ }(E-E_{i})=E-\bigcap_{i\in I}^{ }E_{i}$ $\bigcap_{i\in I}^{ }(E-E_{i})=E-\bigcup_{i\in I}^{ }E_{i}$ Comme l'intersection quelconque d'une famille de parties finies est finie et que la réunion d'une famille finie de parties finie est finie notre résultat suit.
Exercices sur les voisinages
Exercices sur la notion d'intérieur
Exercices sur les ensembles fermés
- Montrer que $A\cap \overline{B} \subseteq \overline{A\cap B}$.
- Sur $\mathbb{R}$ trouver deux ensembles A et B tels que $A\cap \overline{B}$, $B\cap \overline{A}$ ,$\overline{A\cap B}$, et $\overline{A} \cap \overline{B}$ soient tous distincts.
- Donner sur la droite réelle des exemples d'intervalles A et B tels que $A \cap \overline{B}$ ne soit pas contenu dans $\overline{A \cap B}$.
- Soit x un point de $A \cap \overline B$ Montrer que tout voisinage V de x contient un point de $A \cap B$.
- Soit x ∈ $A\cap \overline{B}$ et soit V un voisinage de x, comme A est ouvert il existe un ouvert W contenant x contenu dans A et dans V. W rencontre B en un point y puisque x ∈ $\overline B$ et comme y est dans W y est également dans A, donc y ∈ A∩B.
- Prendre A=$\mathbb{Q}$ et B=$\mathbb{R}$-$\mathbb{Q}$ alors on a : $A\cap \overline {B}=A$, $B\cap \overline {A}=B$, $\overline{A \cap B}=∅$, $\overline{A} \cap \overline{B}=\mathbb{R}$.
-
Prendre A=[0 ; 1] et B =]1 ; 2], alors :
$A \cap \overline{B}=\left \{ 1 \right \}$ et $\overline{A \cap B}=∅$
- Montrer que si A est ouvert A ⊆ α(A) et si A est fermé β(A) ⊆ A.
- Montrer qu'on a toujours α(α(A))=α(A) et β(β(A))=β(A)
- Utiliser A ⊆ $\overline{A}$ et $\overset{o}{A}$ ⊆ A.
- Utiliser 1.
-
Si A est ouvert soit V un voisinage de A contenu dans A, V est donc contenu dans $\overline{A}$ ce qui prouve que x ∈ α(A).
Si A est fermé, β(A) ⊆ $\overline{A}=A$ -
D'après la question précédente puisque α(A) est ouvert on a toujours :
α(A) ⊆ α(α(A)). L'inclusion en sens inverse peut s'écrire $\overset{o}{\beta(\overline{A})}$ ⊆α(A), laquelle résultera de β($\overline{A}$) ⊆ $\overline{A}$ qui est vraie parce que $\overline{A}$ est fermé toujours en vertu de la première question.
- Montrer que pour tout sous-ensemble A de E on a $Fr(\overline{A})\subseteq Fr(A)$ et $Fr(\overset{o}{A})\subseteq Fr(A)$.
- Donner un exemple où les 3 ensembles $Fr(A)$, $Fr(\overset{o}{A})$ et $Fr(\overline{A})$ sont tous distincts.
- A et B étant deux parties quelconques, montrer que Fr(A∪B) ⊆ Fr(A)∪Fr(B)
- Utiliser la définition de Fr(X) conjointement avec $\overline{\overline{X}}=\overline{X}$
- Prendre pour E la droite réelle avec la distance usuelle.
- Utiliser la définition de la frontière et $\overline{A\cup B}=\overline{A}\cup \overline{B}$ .
-
$Fr(\overline{A})=\overline{\overline{A}}\cap \overline{E-\overline{A}}=\overline{A}\cap \overline{E-\overline{A}}$. Il suffit donc de montrer que $\overline{E-\overline{A}}\subseteq \overline{E-A}$ qui résulte de $E-\overline{A}\subseteq E-A$ puisque $A \subseteq \overline{A}$.
Posons maintenant B=E-A de sorte que $\overset{o}{A}=E-\overline{B}$. Il faut donc démontrer que $Fr(E-\overline{B})\subseteq Fr(E-B)$. C'est à dire que $\overline{E-\overline{B}}\cap \overline{E-(E-\overline{B})}\subseteq \overline{E-B}\cap \overline{E-(E-B)}$. C'est à dire encore que $\overline{E-\overline{B}}\cap \overline{\overline{B}}\subseteq \overline{E-B}\cap \overline{B}$, donc que $\overline{E-\overline{B}}\subseteq \overline{E-B}$ puisque $\overline{\overline{B}}=\overline{B}$. Cela résulte du fait que $E-\overline{B}\subseteq E-B$ puisque $B\subseteq \overline{B}$. - Soit A l'ensemble des rationnels contenus dans l'intervalle [0;1], alors $Fr(A)=[0;1]$, $Fr(\overset{o}{A})=∅$, $Fr(\overline{A})=\left \{ 0,1 \right \}$
- $Fr(A\cup B)=\overline{A\cup B}\cap \overline{E-A\cup B}=(\overline{A}\cup\overline{B} )\cap \overline{E-A\cup B }$ D'où nous tirons par distributivité : $Fr(A\cup B)=(\overline{A}\cap \overline{E-A\cup B})\cup (\overline{B}\cap \overline{E-A\cup B}) $ Par ailleurs $E-(A\cup B)\subseteq E-A \Rightarrow \overline{E-A\cup B}\subseteq \overline{E-A}$ et de la même façon : $E-(A\cup B)\subseteq E-B \Rightarrow \overline{E-A\cup B}\subseteq \overline{E-B}$ D'où nous tirons $\overline{A}\cap \overline{E-A\cup B}\subseteq \overline{A}\cap \overline{E-A}=Fr(A)$ et pour la même raison $\overline{B}\cap \overline{E-A\cup B}\subseteq \overline{B}\cap \overline{E-B}=Fr(B)$ d'où finalement : $Fr(A\cup B)\subseteq Fr(A)\cup Fr(B)$
Exercices sur la densité
Soit maintenant x un point quelconque de E s'il n'appartient ni à l'intérieur de A ni à son extérieur il appartient à sa frontière donc tout voisinage V de x rencontre un point de l'un et un point de l'autre, donc un point de la réunion.
Montrer que dans un espace séparable tout sous-ensemble dont tous les points sont isolés est au plus dénombrable.
- B est un recouvrement de E.
- Soient B1 et B2 deux éléments de B et I leur intersection. Pour tout élément x de I, il existe un élément B3 de B contenant x et contenu dans I.
Montrer qu'inversement une famille B possédant cette propriété est toujours la base d'une topologie 'minimale' sur E en un sens que l'on précisera.
Deux éléments de B doivent en particulier être des ouverts donc aussi leur intersection I, qui par définition d'une base doit être une réunion d'éléments de B. Si maintenant x est un élément de I comme I est une réunion d'éléments de B x appartient à au moins un élément de B.
Soit $\mathfrak{T}$ la famille des parties qui sont des réunions d'éléments de B. Alors il résulte immédiatement des hypothèses qu'une réunion quelconque d'éléments de $\mathfrak{T}$ est encore un élément de $\mathfrak{T}$ et que l’intersection de deux éléments de $\mathfrak{T}$ est encore un élément de $\mathfrak{T}$, cela s'étend donc immédiatement aux intersections finies par récurrence.
$\mathfrak{T}$ est en quelque sorte la moins fine des topologies admettant les éléments de B pour ouverts. C'est l'intersection de toutes ces topologies.
Exercices sur les sous-espaces
- Montrer que l'intérieur de B relativement à E est contenu dans l'intérieur de B relativement à A considéré comme sous-espace de E.
- Montrer que si A est ouvert les deux intérieurs de B relativement à E et à A coïncident.
- Tout ouvert de E contenu dans B est également contenu dans A, c'est donc un ouvert de A. D'où notre première proposition.
- Si A est lui-même ouvert les ouverts de A contenu dans B sont exactement les ouverts de E contenus dans B.
Exercices sur la continuité
- f est continue.
- Pour tout sous-ensemble A' de E' $f^{-1}(\overset{o}{A'})\subseteq \overset{o}{\overbrace{f^{-1}(A')}}$.
- Pour tout sous-ensemble A' de E' $\overline{f^{-1}(A')}\subseteq f^{-1}(\overline{A'})$.
Réciproquement soit A' un ouvert, alors $A'=\overset{o}{A'}$, si 2. est vérifiée on a $f^{-1}(A')\subseteq \overset{o}{\overbrace{f^{-1}(A')}}$, donc l'égalité des deux ensembles puisque l'inclusion opposée est toujours vraie. Ce qui prouve que $f^{-1}(A')$ est ouvert et f est continue.
Posant B'=E-A' la condition $f^{-1}(\overset{o}{A'})\subseteq \overset{o}{\overbrace{f^{-1}(A')}}$ est équivalente à $\overline{f^{-1}(B')}\subseteq f^{-1}(\overline{B'})$, d'où l'équivalence 1.⇔3.
- f(x)=-1 pour x < -1
- f(x)=x pour x∈[-1;+1]
- f(x)=+1 pour x > 1
Alors f est continue. Si A'=]-1;+1[ , $f^{-1}(A')=]-1;+1[$, $\overline{A'}=[-1;+1]$, $f^{-1}(\overline{A'})=\mathbb{R}$, $\overline{f^{-1}(A')}=[-1;+1]$
Exercices sur les homéomorphismes
- Soit f l'application de ]0,1[→]0,+∞[ donnée par $f(x)=\frac{1}{x}-1$. Montrer que f est un homéomorphisme mais n'est pas une isométrie.
- Montrer que g:]0,+∞[→$\mathbb{R}$ par $g(x)=x-\frac{1}{x}$ est un homéomorphisme.
- Montrer que ]0,1[ et $\mathbb{R}$ sont homéomorphes.
- Montrer que $\mathbb{R}$ est homéomorphe à tout intervalle ouvert ]a,b[.
- Donner l'expression de la bijection réciproque de f.
- Donner l'expression de la bijection réciproque de g.
- Utiliser les deux questions précédentes.
- Trouver un homéomorphisme linéaire de ]0,1[ sur ]a,b[.
- La bijection réciproque de f est $y \mapsto \frac{1}{y+1}$. f et f-1 sont des fractions rationnelles donc continues. f n'est pas une isométrie car ]0,1[ est borné et ]0,+∞[ ne l'est pas.
- La bijection réciproque de g est $y \mapsto \frac{y+\sqrt{y^{2}+4}}{2}$. L'expression de g et de g-1 correspondent à des fonctions continues de la variable réelle.
- $g\circ f$ donne un homéomorphisme de ]0,1[ sur $\mathbb{R}$.
- l'application h:x→ (b-a)x+a est un homéomorphisme linéaire de ]0,1[ sur ]a,b[. Donc $h\circ f^{-1}\circ g^{-1}$ donne un homéomorphisme de $\mathbb{R}$ sur ]a,b[.
Exercices sur les limites
La suite (x6n)est une suite extraite de (x2n) et de (x3n) si a=lim(x2n) et b=lim(x3n) (x6n) converge donc vers a et vers b d'où a=b.
La suite (x6n+3)est une suite extraite de (x2n+1) et de (x3n) si c=lim(x2n+1) et b=lim(x3n) (x6n+3) converge donc vers c et vers b d'où b=c=a.
En définitive (x2n) et (x2n+1) convergent vers la même limite et il en résulte que la suite (xn) converge également vers cette limite commune.
& \text{ si } (x,y)=(0,0) \text{ alors } f(x,y)=0 \\
& \text{ si } (x,y)\neq (0,0)\text{ alors } f(x,y)=\frac{xy}{x^{2}+y^{2}}
\end{cases}$$.
Soit Fp le sous ensemble de E d'équation y=px privé du point O. Fp est donc une droite passant par l'origine et de pente p, privée de l'origine, donc une droite 'épointée'.
Etudier $\lim_{(x,y)\in F_{p},(x,y)\rightarrow O}f(x,y)$. Qu'en conclure pour la continuité de f en O=(0,0).
Exercices sur les suites de Cauchy
En prenant l'exemple proposé il s'agit de démontrer que ∀ε>0 il existe un entier n0, tel que p,q≥ n0 ⇒ $\left | \frac{p}{1+p}-\frac{q}{1+q} \right |< \varepsilon $. Mais en fait il suffit de démontrer cette inégalité pour ε=1/n où n est un entier strictement positif. Sachant que |p-q|≤p+q pour un couple d'entiers naturels il suffit de montrer que pour p et q suffisamment grands on a $p+q< \frac{1}{n}\left ( 1+p+q+pq \right )$. Cette inégalité résultera elle-même de pq>k(p+q) où k=n(n-1).
On sait de plus que cette suite converge vers +∞ dans la droite réelle achevée $\overline{\mathbb{R}}$, donc elle ne peut converger dans $\mathbb{R}$ à cuase de l'unicité de la limite.
Soit $(F_{n})_{n \in \mathbb{N}}$ une suite décroissante pour l’inclusion de sous-ensembles fermés de E, telle que $\lim_{n\rightarrow \infty }\delta (F_{n})=0$. Montrer que $\bigcap_{n\in \mathbb{N}}^{ }F_{n}$ est un singleton {a}.
L'hypothèse faite sur les Fn montre que pour m≥n xm∈Fn. Soit pour tout n dn=δ(Fn) le diamètre de Fn. La suite dn tend vers 0 dans $\mathbb{R}$. Pour tout ε>0 il existe donc un entier n0tel que n>n0⇒ on ait dn<ε. Il en résulte que pour p et q >n0 on a d(xp,xq)≤ε et (xn) est donc une suite de Cauchy d'éléments de E qui est supposé complet. La suite (xn) converge donc vers un point a∈E. Pour tout p≥n on a xp∈Fp donc xp∈Fn. a est donc la limite d'une suite extraite de (xn) composée de points de Fn et comme Fn est fermé a∈Fn, donc $a\in \bigcap_{n\in \mathbb{N}}^{ }F_{n}$. Supposons maintenant que b soit un autre point de $\bigcap_{n\in \mathbb{N}}^{ }F_{n}$ distinct de a. Si η=d(a,b) choisissons n suffisamment grand pour que δ(Fn)<η/2, mais cela est incompatible avec le fait que a et b appartiennent tous deux à Fn.
Montrer en outre que si f est bijective et si f-1 est continue, alors si E' est complet, E l'est aussi.
Si F est complet, la suite f(xn) converge vers une limite b dans E', alors si a=f-1(b), comme f-1 est supposée continue (xn) converge vers a.
Exercices sur le prolongement
Définissons une fonction f sur E espace métrique avec la métrique usuelle héritée de celle de $\mathbb{R}$ et à valeurs dans $\mathbb{R}$ par $f(x)=\sum_{\varphi (n)< x}^{ }\frac{1}{2^{n}}$, la somme (infinie) étant étendue seulement aux indices n tels que φ(n)<x). Montrer que la restriction de f à l'ensemble B de tous les nombres irrationnels de E est continue, mais qu'elle ne peut être prolongée en une fonction continue sur E.
Maintenant si y est un rationnel de E, alors y=φ(m) pour un certain entier m. et si x et x' sont des éléments de B vérifiant x<y<x', on a toujours f(x')≥f(x)+1/2m, ce qui prouve que l'oscillation de f en y relativement à B n'est pas nulle et que f ne peut être prolongée de façon continue au point y.
Exercices sur les espaces compacts
λ1 un indice tel que x0∈Uλ1
λ2 un indice tel que x1∈Uλ2
........................
λn0 un indice tel que xn0-1∈Uλn0
Posons H={λ0,λ1,λ2,...,λn0}, alors $\bigcup_{\lambda \in H}^{ }U_{\lambda }$ est un recouvrement fini de F extrait de $\bigcup_{\lambda \in L}^{ }U_{\lambda }$.
Pour tout recouvrement ouvert (Uλ) de E ∃α>0 tel que toute boule ouverte de rayon α soit contenue dans au moins un des Uλ.
- E est compact
- Toute suite décroissante d'ensembles fermés non vides a une intersection non vide.
-
1.⇒2.
Considérer une suite (xn) avec xn∈Fn ∀n -
2.⇒1.
Soit (xn) une suite quelconque et Fn l'adhérence de {xn,xn+1, ....}
-
1.⇒2.
Soit (Fn) une suite décroissante de fermés, et soit donc une suite (xn) avec xn∈Fn ∀n si E est compact cette suite possède une valeur d'adhérence a. Tous les xn sont dans F0 qui est fermé, donc a est dans $\overline{F_{0}}$, mais a est aussi une valeur d'adhérence de la suite (xn+1) pour la même raison donc a∈F1. En définitive a est dans tous les Fn et l'intersection de cette suite est non vide. -
2.⇒1.
Soit (xn) une suite quelconque de points de E. Posons En={xn,xn+1, ...} et Fn=$\overline{E_{n}}$. Les Fn forment une suite décroissnte de fermés de E, leur intersection contient donc un point a. Il est clair que a est une valeur d'adhérence de la suite (xn).
Exercices sur les ensembles compacts
Exercices sur les espaces localement compacts
Soit (E,$\mathfrak{T}$) un espace localement compact et V un ouvert de E ; montrer que V est localement compact.
$K'\subseteq W'=\bigcup_{i=1}^{n}W'_{x_{i}}$, posant alors $W=\bigcap_{i=1}^{n}W_{x_{i}}$ on a bien construit des ouverts séparant a et K'. Soit alors H un voisinage compact de a alors H'=H∩(E-W') est un fermé de H, donc un compact et H'⊆V.
Soit (E,$\mathfrak{T}$) un espace topologique localement compact et ∞ un élément n'appartenant pas à E. On pose $\widehat{E}=E\cup \left \{ \infty \right \}$. On appelle 'ouvert' de $\widehat{E}$ tout sous-ensemble U de $\widehat{E}$ qui est soit un ouvert de E, soit la réunion de {∞} et du complémentaire d'une partie compacte de E.
- Montrer que les 'ouverts' de $\widehat{E}$ ainsi définis forment une topologie $\mathfrak{T'}$ sur $\widehat{E}$.
- Montrer que la topologie induite par $\mathfrak{T'}$ sur E est $\mathfrak{T}$. Montrer que si (E,$\mathfrak{T}$) n'est pas compact, alors E est dense dans ($\widehat{E}$,$\mathfrak{T'}$).
- Montrer que ($\widehat{E}$,$\mathfrak{T'}$) est compact.
- Commencer par montrer que l'intersection de deux ouverts de $\mathfrak{T'}$ est encore un élément de $\mathfrak{T'}$.
- Que se passe-t-il si l'intersection avec E d'un voisinage de ∞ est vide ?
- Partir d'un recouvrement ouvert de $\widehat{E}$ et isoler un ouvert qui contient ∞
-
Soient U et V deux ouverts de $\widehat{E}$, alors il y a 3 possibilités:
- Soit U et V ne contiennent pas ∞ alors leur intersection est un ouvert de E, donc un ouvert de $\widehat{E}$.
- Soit U et V contiennent ∞ alors U=(E-K1)∪{∞} V=(E-K2)∪{∞} dans ce cas U∩V=(E-K1∪K2)∪{∞} donc U∩V est un ouvert parce que K1∪K2 est compact.
- Soit l'un des deux, disons U contient ∞ et pas l'autre. Alors U∩V=V.
On conclut par récurrence sur le nombre d'ouverts pour traiter le cas fini en toute généralité.
Pour ce qui concerne les réunions il est clair qu'une réunion quelconque d'ouverts de E est encore un ouvert de E à cause des axiomes d'une topologie. Une réunion d'ensembles de la forme (E-Ki)∪{∞} est de la forme $(E-\bigcap_{i}^{ }K_{i})\cup \left \{ \infty \right \}$. Donc de la même forme parce qu'une intersection quelconque de compacts est encore un compact. Pour finir la réunion de l'ouvert V de E avec (E-K)∪{∞} est {∞}∪(E-K∩(E-V)) donc un ouvert de $\widehat{E}$, parce que E-V étant fermé K∩(E-V) est fermé dans K donc compact puisque K l'est. Dans le cas général il suffit d'utiliser l'associativité de la réunion. En définitive toute réunion d'ouverts est un ouverts. Pour finir il est clair que ∅ est ouvert dans $\widehat{E}$ parce qu'il est ouvert dans E, et que $\widehat{E}$ est ouvert car égal à (E-∅)∪{∅} et que ∅ est compact dans E. -
Les intersections avec E des ouverts de $\widehat{E}$ sont soit des ouverts de E soit des ensembles de la forme E-K où K est un compact, donc un fermé ; dans tous les cas ce sont des ouverts. réciproquement tout ouvert V apparaît comme l'intersection avec E de V considéré comme ouvert de $\widehat{E}$. $\widehat{E}$ induit bien sur E la topologie initiale $\mathfrak{T}$.
Soit V un voisinage ouvert de ∞ dans $\widehat{E}$, alors V∩E=E-K où K est un compact si E-K est vide c'est que E=K donc que E est compact. - Soit (Vi) un recouvrement ouvert de $\widehat{E}$. Il existe au moins un des Vi qui contient ∞. Soit donc i0 un indice tel que ∞∈Vi0 On a donc Vi0∩E=E-Ki0 où Ki0 est un compact. Les Vi forment en particulier un recouvrement de Ki0, on peut donc en extraire un recouvrement fini, en adjoignant Vi0 à ce recouvrement, on obtient un recouvrement fini de $\widehat{E}$ extrait de (Vi).
Exercices sur la connexité
$\mathfrak{T}$1 = {∅, {b}, {b, c}, X} et $\mathfrak{T}$2 = {∅, {b}, {c}, {a, c}, {b, c}, X} ?
Déterminer les composantes connexes de X pour ces topologies.
Pour la topologie $\mathfrak{T}$2 on a un recouvrement par les ouverts {a,c} et {b} qui sont tous deux non vides. L'espace n'est donc pas connexe. La topologie induite sur {a,c} par $\mathfrak{T}$2 est {∅,{c},{a,c}} cet ensemble est donc connexe. La composante connexe de a C(a) contient donc c, mais pas b car alors X serait connexe. Il en résulte que C(a)=C(c)={a,c} et donc C(b)={b}
sont-elles connexes : $\overset{o}{A}$, Fr(A) ?
Si A est la réunion de deux disques fermés tangents alors A est connexe car chacun des deux disques fermés est connexe car convexe et que les deux disques ont un point commun. Par contre l'intérieur de A est la réunion de deux disques ouverts disjoints, $\overset{o}{A}$ a donc deux composantes connexes distinctes et n'est pas connexe.
Exercice sur les espaces produits
- Montrer que si (a,b) est une valeur d'adhérence de ((xn,yn)), alors a est une valeur d'adhérence de (xn) et b est une valeur d'adhérence de (yn)
- Montrer que réciproquement il peut arriver que ((xn,yn)) n'ai pas de valeur d'adhérence alors que (xn) et (yn) en aient chacune une.
- Cela résulte de la définition d'une valeur d'adhérence et de ce résultat.
- Il est clair qu'en prenant les suites (xn) et (yn) données dans l'aide chacune de ces deux suites possède 0 comme valeur d'adhérence, mais qu'aucune suite extraite de ((xn,yn)) n'est convergente.
- Pour que la suite (xm)m≥1 converge vers a=(an), il faut et il suffit que pour chaque n la suite (xm,n)m≥1 converge vers an
- Pour que la suite (xm)m≥1 soit une suite de Cauchy dans E, il faut et il suffit que pour tout n (xm,n)m≥1 soit une suite de Cauchy dans En.
- E complet ⇔ chaque En est complet.
- E est précompact ⇔ Chaque En est précompact.
- E est compact ⇔ Chaque En est compact.
- E est connexe ⇔ Chaque En est connexe.
- D'après P si (xm)m≥1 converge vers a chaque suite (xm,n)m≥1 pour n≥1 converge vers la limite an=pn(a). Réciproquement supposons que pour chaque n (xm,n)m≥1 converge vers an et soit a=(an). Soit ε≥0. Soit m0 un entier suffisamment grand pour que $\sum_{n_{0}+1}^{\infty }\frac{1}{2^{n}}< \epsilon /2$ . Pour chaque i entre 1 et m0, il existe un entier mi, tel que m≥mi⇒ di(xm,i,ai)≤ε/2m0. Si Si M est plus grand que m0 et chacun des mi on a d(xm,a)≤ε dès que m>M et la suite (xn) converge bien vers a.
- La proposition P affirme que la condition est nécessaire. Supposons réciproquement que pour tout indice n (xm,n) soit une suite de Cauchy. Soit ε>0. on choisit m0 comme précédemment. Pour chaque i entre 1 et m0, il existe un entier mi, tel que m≥mi et m'≥mi ⇒ di(xm,i,xm',i)≤ε/2m0.Si Si M est plus grand que m0 et chacun des mi on a d(xm,xm')≤ε dès que m et m' sont >M. donc (xm) est une suite de Cauchy.
- 3. résulte de 1. et 2.
- D'après la proposition P il suffit qu'un des En soit précompact pour que E le soit. Si V est un ensemble quelconque du produit E et de diamètre δ sa projection sur En est de diamètre au plus égal à δ×2n, donc à partir d'un recouvrement de E par des ensembles de diamètre ε on peut fabriquer un recouvrement de En par des ensembles de diamètre ε×2n.
- 5. résulte de 3. et 4.
- La condition est nécessaire à cause de la proposition P et du fait que l'image d'un connexe par une application continue est connexe. Elle est suffisante par ce que si un En, disons E1 par exemple est non connexe, et si U,V est une partition de E1 en deux ouverts non vides disjoints, alors les deux ensembles U×E2×...×En× ..... et V×E2×...×En× ..... forment un recouvrement de E par deux ouverts disjoints non vides.
Exercices sur les points fixes
Montrer également que toute suite récurrente du type xn+1=f(xn), de terme initial quelconque converge vers le point fixe de f.
Soit y=f(x*)=f(fq(x*))=fq(f(x*))=fq(y)=f(x*)=y.
Donc y=x* et y est fixe pour f.
x0 étant un point quelconque de E, la suite des xn=fn(x0) converge vers x*, car chacune des q sous-suites xnq+r pour 0≤r≤q-1, converge vers x*.
Posons F=ℝ*=ℝ-{0} alors f est une application contractante de F dans F n'admettant aucun point fixe dans F.
