Exercices sur les espaces vectoriels topologiques
∀λ∈K,∀v∈U |λ|≤1⇒λv∈U
- Montrer qu'un sous-espace vectoriel F de E est toujours équilibré.
- Montrer que la réunion de parties équilibrées est équilibrée.
Si A est une partie de E, on appelle noyau équilibré de A (notation N(A)) la réunion de toutes les parties équilibrées contenues dans A.
- Montrer que N(A) est équilibrée, non vide et contenue dans A. N(A) est la plus grande partie équilibrée contenue dans A.
- Montrer que si v est un vecteur quelconque de E, pour que v∈N(A)
- Montrer que le noyau équilibré de tout voisinage de 0 est un voisinage de 0. Plus précisément tout ouvert contenant le vecteur nul contient un ouvert équilibré contenant le vecteur nul.
il faut et il suffit que pour tout scalaire λ vérifiant |λ|≤1 on ait λv∈A.
- Revoir la définition d'un sous-espace vectoriel.
- Soient A et B équilibrées et v∈A∪B, supposer d'abord que v∈A.
- Toute partie équilibrée contient forcément le vecteur nul.
- Utiliser la continuité de la multiplication externe au point (0K,0E)
- Si F est un sous-espace de E et si v est un vecteur de F alors λv ∈F donc a fortiori si |λ|≤1.
- Si v∈A et si |λ|≤1 alors λv∈A donc λv∈A∪B, même chose si v∈B.
- N(A) est non vide car 0∈N(A). La réunion de parties de A reste une partie de A. Il est clair que N(A) contient toute partie équilibrée contenue dans A par sa définition même.
- En effet, v appartient à N si et seulement si, parmi les parties équilibrées contenant v, au moins l'une d'entre elles est incluse dans A, ou encore si la plus petite d'entre elles, {λv ; |λ| ≤ 1}, est incluse dans A.
- En effet, soit O un ouvert contenant le vecteur nul. La multiplication externe étant continue au point (0K,0E)
il existe un réel α>0 et un ouvert W contenant le vecteur nul tels que : $|\lambda |< \alpha \ , y\in W \Rightarrow \lambda y\in O$
L'ensemble Ω, défini comme suit, est alors un ouvert équilibré inclus dans O :
$\Omega=\bigcup_{0< |\lambda |< \alpha }^{ }\lambda W $
De plus cette réunion est non vide (et contient 0) car K est non discret.
Exercices sur les espaces normés et espaces de Banach
$\left ( \sum_{k=1}^{n}|a_{k}+b_{k}|^{p} \right )^{\frac{1}{p}}\leq
\left ( \sum_{k=1}^{n}|a_{k}|^{p} \right )^{\frac{1}{p}}+
\left ( \sum_{k=1}^{n}|b_{k}|^{p} \right )^{\frac{1}{p}}$
Cette inégalité est évidente quand p=1 on peut donc supposer que p>1.
La preuve de l'inégalité de Minkowski dépend elle même de l'inégalité de Hölder.
$\sum_{k=1}^{n}|a_{k}b_{k}|\leq \left ( \sum_{k=1}^{n}|a_{k}|^{p} \right )^{\frac{1}{p}}\left ( \sum_{k=1}^{n}|b_{k}|^{q} \right )^{\frac{1}{q}}$ où les nombres p et q vérifient l'égalité $\frac{1}{p}+\frac{1}{q}=1$
En effet partant de l'identité (|a|+|b|)p=(|a|+|b|)p-1|a|+(|a|+|b|)p-1|b| et posant a=ak, b=bk et sommant pour k allant de 1 à n, nous obtenons :
$\sum_{k=1}^{n}\left ( |a_{k}|+|b_{k}| \right )^{p}=\sum_{k=1}^{n}\left ( |a_{k}|+|b_{k}| \right )^{p-1}|a_{k}|+\sum_{k=1}^{n}\left ( |a_{k}|+|b_{k}| \right )^{p-1}|b_{k}|$
Appliquant maintenant l'inégalité de Hölder aux deux sommes du membre de droite, et en se souvenant que (p-1)q=p, il vient :
$\sum_{k=1}^{n}\left ( |a_{k}|+|b_{k}| \right )^{p}\leq \left ( \sum_{k=1}^{n}\left ( |a_{k}|+|b_{k}| \right )^{p} \right )^{1/q}\left ( \left [ \sum_{k=1}^{n}|a_{k}|^{p} \right ]^{1/p} +\left [ \sum_{k=1}^{n}|b_{k}|^{p} \right ]^{1/p}\right )$
et en divisant les deux membres par $\left ( \sum_{k=1}^{n}\left ( |a_{k}|+|b_{k}| \right )^{p} \right )^{1/q}$
nous obtenons :
$\left ( \sum_{k=1}^{n}(|a_{k}|+|b_{k}|)^{p} \right )^{\frac{1}{p}}\leq
\left ( \sum_{k=1}^{n}|a_{k}|^{p} \right )^{\frac{1}{p}}+
\left ( \sum_{k=1}^{n}|b_{k}|^{p} \right )^{\frac{1}{p}}$
qui donne Minkowski par application de l'inégalité du triangle dans K.
$\sum_{k=1}^{n}|a_{k}b_{k}|\leq \left ( \sum_{k=1}^{n}|a_{k}|^{p} \right )^{\frac{1}{p}}\left ( \sum_{k=1}^{n}|b_{k}|^{q} \right )^{\frac{1}{q}}$ où les nombres p et q vérifient l'égalité $\frac{1}{p}+\frac{1}{q}=1$
Nous commençons par remarquer que l'inégalité de Hölder est homogène c'est à dire que si elle est valide pour deux points (a1,...,an) et (b1,...,bn) alors elle est valide pour (λa1,...,λan) et
(μb1,...,μbn) pour tout couple de scalaires λ,μ. On peut donc se contenter de prouver l'inégalité de Hölder pour le cas particulier $\sum_{k=1}^{n}|a_{k}|^{p}=\sum_{k=1}^{n}|b_{k}|^{p}=1$.
Sur l'image suivante on voit le graphe de la courbe y=xp-1 un point A(a,0) est situé sur l'axe des abscisses et un point B(0,b) est situé sur l'axe des ordonnées.
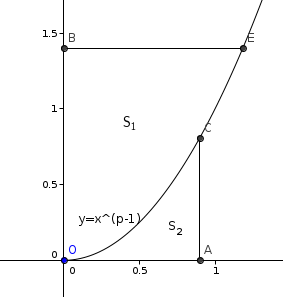
On considère les deux aires:
$S_{1}=\int_{0}^{a}x^{p-1}dx=\frac{a^{p}}{p}$
$S_{2}=\int_{0}^{b}x^{q-1}dx=\frac{b^{q}}{q}$
Il est clair sur la figure que S1+S2≥ab
Il en résulte que $ab<\frac{a^{p}}{p}+\frac{b^{q}}{q}$
En appliquant cela à chacun des ak et des bk et en sommant sur k nous obtenons dans le cas particulier étudié :
$\sum_{k=1}^{n}|a_{k}b_{k}|\leq 1$
- Montrer que E est muni d'une structure d'espace vectoriel.
- Montrer que si pour toute f∈E on pose $||f||_{1}=\int_{a}^{b}|f(t)|dt$, || ||1 est une norme sur E.
Dans toute la suite on suppose I=[0;1].Pour tout entier n≥1 on définit ainsi la fonction fn de :
$$
\begin{cases}
& \text{si x} \in [0,1/2] f(x)=1 \\
& \text{si x} \in [1/2+1/n,1] f(x)=0 \\
& \text{si x}[1/2,1/2+1/n] f(x)=α_{n}x+β_{n}
\end{cases}
$$
avec des constantes αn et βn que l'on ajustera pour assurer la continuité.
- Montrer que (fn) est une suite de Cauchy dans E
- Montrer que E n'est pas un espace de Banach.
- L'addition et la multiplication par un scalaire sont les opérations usuelles sur les fonctions à valeurs réelles.
- Le seul point non évident est l'inégalité du triangle.
- Donner une majoration de ||fp-fq||1 pour p,q≥n.
- Montrer que la suite fn ne peut être convergente dans l'espace E.
- La somme de deux fonctions continues est encore continue. Si f est continue alors pour tout scalaire λ la fonction λf est encore continue.
- ||f+g||1≤||f||1+||g||1 résulte de |f(x)+g(x)|≤|f(x)|+|g(x)| et du fait que $f:\rightarrow \int_{a}^{b}f(x)dx$ est croissante.
- ||fp-fq||1≤1/2n pour p,q≥n. Il en résulte qu'on a bien une suite de Cauchy
- Si f est la limite des fn on a forcément f(x)=1 pour tout x∈[0,1/2] et f(x)=0 pour tout x∈]1/2,1]. f ne peut donc être continue en 1/2.
- Montrer que si l'un des deux ensembles A,B est ouvert, A+B est ouvert.
- Montrer que si A et B sont tous deux compacts, A+B est compact.
- Montrer que si A est compact et B fermé, alors A+B est fermé.
- Donner un exemple de deux sous-ensembles A et B fermés tels que A+B ne soit pas fermé.
- Pour chaque a de A {a}+B est ouvert car homéomorphe à B.
- Utiliser le fait que le produit de deux compacts est compacts.
- Soit x un point de l'adhérence de A+B, considérer une suite an de points de A et une suite bn de points de B tels que x=lim (xn=an+bn).
- Prendre E=$\mathbb{R}$ et A=$\mathbb{N}$
- $A+B=\bigcup_{a\in A}^{ }\left \{ a \right \}+B$ est donc ouvert comme réunion d'ouverts.
- A×B est compact et (x,y)→x+y est continue de A×B sur A+B.
- Soit donc x comme il est dit dans l'aide. Extrayons de la suite an une suite yn=apn convergente vers un point a de A. Soit alors zn=bpn. Comme zn=xpn-yn alors zn converge vers un point b de B qui est fermé. On a donc x=a+b et A+B est bien fermé.
- Si B est l'ensemble des nombres de la forme -n+1/n pour n≥1 A+B contient tous les nombres de la forme 1/n mais ne contient pas leur limite 0.
Exercices sur les séries dans un espace normé
Définir de même sin(z), cos(z), sh(z), ch(z).
On définit de même les fonctions sin, cos, sh et ch par les sommes des séries représentant ces fonctions pour la variable réelle en substituant z à x, par exemple $cos(z)=\sum_{n=0}^{\infty }(-1)^{n}\frac{z^{2n}}{(2n)!}$.
- Montrer que ||x|| est une norme sur E, et que E, muni de cette norme est un espace de Banach.
- Soit pour tout entier m≥0, em la suite (εm,n) de points de E où εm,n=0 si m≠n et εn,n=1. Montrer que pour tout point x=(xn) de E la série $\sum_{n=0}^{\infty }x_{n}e_{n}$ est commutativement convergente dans E et de somme x.
- Montrer que la série $\sum_{n=0}^{\infty }x_{n}e_{n}$ n'est pas toujours absolument convergente.
- Le fait qu'on ait un espace normé est évident, il faut seulement montrer la complétude.
- Majorer la norme de sn-x où sn est la n-ième somme partielle de la série.
- Considérer le cas où la série (xn) n'est pas absolument convergente dans $\mathbb{R}$
- E est un sous-espace fermé de l'espace de Banach de toutes les suites bornées de nombres réels.
- ||x-sn||=supi≥n|xi| or dans cette égalité le membre de droite tend vers 0 d'après la définition de l'espace E. Soit σ est une bijection de $\mathbb{N}$ et si ε un nombre réel positif. Soit maintenant n0 tel que ||sn-x||≤ε pour n≥n0. Si n1=Sup σ-1({0,1,...,n}) et si $s'_{n}=\sum_{i=0}^{n}x_{\sigma (i)}e_{\sigma (i)}$ dès que n≥n1, on a ||s'n-x||≤ε d'où notre proposition.
- Si $x=(\frac{1}{n+1})_{n\in \mathbb{N}}$ la série n'est pas absolument convergente.
- Pour toute série (un) de nombres réels non absolument convergente, il est possible de réarranger les termes de façon à ce que la série converge vers n'importe quelle limite donnée b à l'avance. Plus précisément, il existe une permutation n → p(n) de telle que la série de terme général up(n) converge vers b.
- En déduire que toute série de réels commutativement convergente est absolument convergente.
- Généraliser au cas de suites de $\mathbb{R}$n.
- Généraliser au cas des espaces de dimension finie.
- En effet s'il n'existe qu'un nombre fini de valeurs de n pour lesquelles un≤0 alors la série (un) est absolument convergente à partir d'un certain rang, donc absolument convergente. La même remarque vaut pour les termes positifs.
Si (un) n'est pas absolument convergente on peut en extraire deux séries infinies dont tous les termes ont même signe:- Une série s+ dont le terme général est la suite extraite de u formée des termes strictement positifs dans l'ordre dans lequel ils se présentent.
- Une série s- dont le terme général est la suite extraite de u formée des termes négatifs ou nuls dans l'ordre dans lequel ils se présentent.
Ces deux séries sont divergentes car la convergence de l'une d'elle entraîne la convergence de l'autre et la convergence absolue de (un). En outre le terme général de chacune d'elle tend vers 0 car un tend vers 0.
Soit (p0,p1, ... ,pn, ...) la suite croissante des indices des un tels que un >0. Posons vi=upi ∀ i ∈ $\mathbb{N}$.
Soit (q0,q1, ... ,qn, ...) la suite croissante des indices des un tels que un ≤0. Posons wi=uqi ∀ i ∈ $\mathbb{N}$.
On remarquera que les deux ensembles {p0,p1, .. ,pn, ..} {q0,q1, ...,qn, ... } forment une partition de $\mathbb{N}$.
Supposons par exemple b≥0.
On définit maintenant une suite d'entiers φ(n) par récurrence de la façon suivante:
φ(0)=p0
Si up0<b φ(1)=p1, sinon φ(1)=q0.
Si uφ(0)+uφ(1)<b φ(2) sera le plus petit élément de {p0,p1, .. ,pn, ..} non encore choisi, sinon le plus petit élément de {q0,q1, ...,qn, ... } non encore choisi, et ainsi de suite. On voit ainsi que la série de terme général uφ(n) passe alternativement au dessus et en dessous de b que la différence de la somme partielle d'indice n de cette série avec b tend vers 0 puisque les deux suites vn et wn tendent vers 0.
Le fait que φ est une bijection résulte du fait que les deux ensembles {p0,p1, .. ,pn, ..} {q0,q1, ...,qn, ... } forment une partition de , et qu'on 'épuise' ainsi tous les pi et tous les qi.D'où le résultat. - La seconde proposition n'est que la contraposée de la première.
- Cela résulte du fait que les n projections de $\mathbb{R}$n sur $\mathbb{R}$ sont continues
- Si E est de dimension finie, le choix d'une base permet de réaliser un isomorphisme de E sur $\mathbb{R}$n
Exercices sur les séries multiples
um,n=0 sauf si m=n auquel cas um,n =1 ou bien n=m+1 auquel cas um,n=-1.
Voici la représentation de cette suite avec n en abscisses et m en ordonnées.
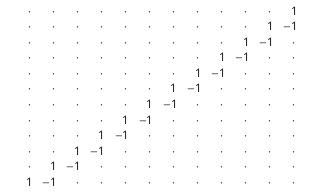
Montrer que le théorème d'associativité ne s'applique pas pour cette série (qui n'est pas absolument sommable).
Montrer que toute famille sommable possède la propriété de Cauchy, à savoir que :
Quel que soit ε>0 il existe une partie finie J0 de I, telle que pour toute partie finie K de I contenant J0 on ait $||\sum_{i\in K} x_{i}||\leq \epsilon$.
En déduire que si (xi)i∈I est une famille sommable l'ensemble D des indices i tels que xi≠0 est au plus dénombrable.
Soit donc Dn comme il est dit dans l'aide, et soit Jn une partie finie de I telle que pour toute partie finie K de I contenant Jn on ait$||\sum_{i\in K} x_{i}||\leq 1/n$. Alors Dn ⊆ Jn et donc Dn est fini. Comme $D=\bigcup_{n\geq 1} D_{n}$ il en résulte que D est au plus dénombrable.
Exercices sur les sous-espaces d'un espace normé
Soit I un intervalle compact de la droite réelle, par exemple I=[0,1].
On considère l'espace E=$\mathfrak{C}$(I) de toutes les applications continues sur I à valeurs réelles. Ces applications sont en particulier bornées et on peut considérer la norme ||f||=Supx∈I|f(x)|, E devient donc un espace vectoriel normé et même un espace de Banach dans la mesure où toute limite uniforme de fonctions continue sur I est encore continue sur I.
Nous nous proposons ici de montrer qu'une certaine famille dénombrable de polynômes, les polynômes dits de Bernstein est une famille totale dans l'espace E.
Ponr tout entier n et tout entier k≤n on pose $B_{n,k}(x)=\binom{n}{k}x^{k}(1-x)^{n-k}$
- Effectuer les calculs suivants :
$\sum_{k=0}^{n}B_{n,k}(x)$,
$\sum_{k=0}^{n}kB_{n,k}(x)$,
$\sum_{k=0}^{n}k^{2}B_{n,k}(x)$ - Soit α>0 et x∈[0,1] on pose : $A=A(\alpha ,x)=\left \{ k\in \left [ 0,n \right ]|\frac{k}{|n-x|}\geq \alpha \right \}$
Montrer que $\sum_{k\in A}B_{n,k}(x)\leq \frac{1}{4n\alpha ^{2}}$ - Pour toute f∈E nous posons $f_{n}(x)=\sum_{k=0}^{n}f(\frac{k}{n})B_{n,k}(x)$.
Montrer que la suite (fn) converge uniformément vers f sur [0,1].
- Développez (x+(1-x))n
$k\binom{n}{k}=n\binom{n-1}{k-1}$
$\sum_{k=0}^{n}k^{2}B_{n,k}(x)=\sum_{k=0}^{n}k(k-1)B_{n,k}(x)+\sum_{k=0}^{n}kB_{n,k}(x)$ - Par définition de A et compte tenu du fait que les Bn,k sont positifs et que A⊆[1,n], nous avons :
$n^{2}\alpha ^{2}\sum_{k\in A}B_{n,k}(x)\leq \sum_{k\in A}(k-nx)^{2}B_{n,k}(x)\leq \sum_{k\in [0,n]}(k-nx)^{2}B_{n,k}(x)$ - ∀ε>0 par l'uniforme continuité de f sur I il existe α>0 tel que |x-y|≤α ⇒ |f(x)-f(y)|≤ε .
- Il résulte des indications données dans l'aide que :
$\sum_{k=0}^{n}B_{n,k}(x)=1$
$\sum_{k=0}^{n}kB_{n,k}(x)=nx$
$\sum_{k=0}^{n}k^{2}B_{n,k}(x)=nx(1+(n-1)x)$ - Compte tenu des résultats de la première question, de l'inégalité donnée dans l'aide et que dans l'intervalle I nous avons x(1-x)≤1/4), il vient :
$n^{2}\alpha ^{2}\sum_{k\in A}B_{n,k}(x)\leq nx(1-x)$
$\sum_{k\in A}B_{n,k}(x)\leq \frac{1}{4n\alpha ^{2}}$ - Soient donc ε et α comme il est dit dans l'aide et posons B=[1,n]-A.
Compte tenu de la définition de fn il vient :
$|f(x)-f_{n}(x)|\leq \sum_{k\in A}|f(x)-f(k/n)|B_{n,k}(x)+\sum_{k\in B}|f(x)-f(k/n)|B_{n,k}(x)$
puis :
$|f(x)-f_{n}(x)|\leq 2||f||\sum_{k\in A}B_{n,k}(x)+\sum_{k\in B}\epsilon B_{n,k}(x)\leq \frac{||f||}{2n\alpha ^{2}}+\epsilon$
Pour n assez grand $\frac{||f||}{2n\alpha ^{2}}\leq \epsilon$ et |f(x)-fn(x)|≤2ε, CQFD.
- Montrer que si F est un sous-espace de dimension finie de E, en somme directe avec V (V∩F={0}) alors V+F est fermé dans E.
- Montrer que tout sous-espace de dimension finie de E est fermé dans E.
Soit maintenant une suite convergente de points yn+λnx de V+Kx et soit z sa limite. Compte tenu de ce qui précéde la suite λn est une suite convergente dans K vers un scalaire λ. Il en résulte donc que yn=z-λnx converge vers z-λx. Or comme V est fermé ce vecteur appartient à V. En définitive z appartient à V+Kx et cet ensemble est fermé.
En raisonnant par récurrence sur la dimension de F on montrer maintenant que V+F est fermé si F est de dimension finie et V fermé.
Comme {0} est fermé il en résulte que si F est de dimension finie F={0}+F est fermé.
Exercices sur les produits finis d'espaces normés
Il en résulte que F∩G={0}.
Pour tout x de E on peut écrire x=p(x)+(x-p(x)).
Or p(x-p(x))=p(x)-p²(x)=p(x)-p(x)=0 et donc E=F+G.
p étant supposée continue le résultat suit d'après la définition d'un supplémentaire topologique.
Montrer que dans un espace normé une boule ne peut contenir une droite.
Pour la topologie produit tout ouvert contenant un point disons (0,0,0,.....) contient au moins une droite. Cela résulte de la définition de la topologie produit.
Exercices sur les applications multilinéaires continues
- Vérifier que ||P|| est bien une norme sur E.
- Montrer que u:E→E est une application linéaire continue.
- Montrer que v:E→E n'est pas continue.
- Utiliser l'inégalité du triangle dans $\mathbb{R}$.
- Calculer ||u(P)|| en fonction de ||P||
- Trouver une suite (Pn) de polynômes tendant vers 0 telle que (v(Pn)) ne tende pas vers 0.
- Supposons d°(Q)≤d°(P) alors en posant n=d°(Q) on peut écrire $P=\sum_{k=0}^{n}a_{k}X^{k}$ et $Q=\sum_{k=0}^{n}b_{k}X^{k}$ où les coefficients de P d'ordre >d°(P) sont tous nuls. On a alors $P+Q=\sum_{k=0}^{n}(a_{k}+b_{k})X^{k}$. De la relation |ak+bk|≤|ak|+|bk| nous tirons ||P+Q||≤||P||+||Q||.
- De la définition de u et de la norme nous concluons ||u(P)||=||P||. la continuité de u en résulte.
- Posons Pn(X)=Xn/n, alors la suite (Pn) tend vers 0. Cependant on a ||v(Pn)||=1, ce qui prouve que v n'est pas continue.
Montrer qu'il y a équivalence entre :
- u est bornée sur la boule unité fermée B de E.
- u est bornée sur la sphère unité S de E.
- u est continue.
2.⇒3 car si x=(x1, ... ,xn) est un vecteur quelconque de E dont aucune composante n'est nulle et si M =Supx∈S ||u(x)|| et si y=(x1/||x1||,...,xn/||xn||) alors y∈S, donc ||u(y)||≤M ce qui peut encore s'écrire ||u(x)||≤M||x1||.||x2||...||xn||. Cette inégalité est vraie a fortiori si une des composantes de x est nulle puisqu'alors u(x)=0.
3.⇒1. en appliquant la caractérisation des applications multilinéaires continues.
Exercices sur les algèbres de Banach
De plus les vecteurs Xj=(δ1,j, ...,δn,j) où δi,j=0 si i≠j et δi,j=1 si i=j sont tous de norme 1. Il résulte donc de la définition de ||A|| que ce nombre est supérieur à la norme de chacun des vecteurs A.Xj, mais le vecteur A.Xj est égal à la j-ième colonne de la matrice A. Il en résulte que ||A|| est supérieur ou égal à chacun des nombres $\sqrt{\sum_{i=1}^{n}\alpha _{i,j}^{2}}$ or l'un de ces nombres est forcément supérieur à s(A), d'où la démonstration du résultat donné dans l'aide.
le fait que A→||A|| soit une norme est à peu près évident. En particulier si ||A||=0 il en résulte que les vecteurs A.Xj sont tous nuls et comme les Xj forment une base de Kn, A est nul. Il résulte de la définition de ||A|| que pour tout vecteur X on a ||AX||≤||A||.||X||, de là nous concluons que
||(AB).X||=||A(BX)||≤||B||.||AX||≤||B||.||A||.||X|| et donc ||(AB).X||≤||A||.||B|| si ||X||≤1 d'où ||AB||≤||A||.||B|| compte tenu, cette fois encore de la définition de la norme.
Le fait que E soit complet résulte du fait que si (An=αi,j,n) est une suite de Cauchy de matrices de E, compte tenu du résultat de l'aide pour tout couple (i,j) chaque suite (αi,j,n) est une suite de Cauchy de scalaires donc convergente vers un élément αi,j de K. La matrice A=(αi,j) est alors la limite de la suite (An).
Oo obtient de même la relation à l'ordre n+1 à partir de la relation à l'ordre n par multiplication à droite par y et par substitution.
Nous aurions donc l'inégalité (n+1)||yn||≤2||x||.||y||.||yn|| pour tout valeur de n qui entraine yn=0 pour n suffisamment grand. Mais la relation yn=0 entraine yn-1=0 compte tenu de xyn-ynx=nyn-1, et par récurrence descendante y=0 ce qui est impossible.
Exercices sur les normes équivalentes
La convergence de (xn) vers x pour une quelconque norme || || équivaut à la convergence de ||xn-x|| vers 0.
Etant donné ε>0 et η>0 tels que ||x-y||1≤η⇒||f(x)-f(y)||1≤ε on a ||f(x)-f(y)||2≤bε dès que ||x-y||2≤η/a .
Exercices sur les espaces d'applications multilinéaires continues
- Soit u une application linéaire continue de E dans $\mathbb{R}$. Si u(en)=ηn, montrer que la série Σηn est absolument convergente, et que, dans l'espace de banach E'=$\mathfrak{L}$(E,$\mathbb{R}$) $||u||=\sum_{n=0}^{\infty }\left | \eta _{n} \right |$.
L'espace E' défini plus haut est l'espace $\mathfrak{l}$1 de Banach. - E' est, du point de vue algébrique un sous-espace vectoriel de E. Montrer que la norme de $\mathfrak{l}$1 n'est pas équivalente à la norme induite par celle de c0.
- Montrer que l'espace $E"=\mathfrak{L}(E';\mathbb{R})$ s'identifie avec l'espace des suites bornées de nombres réels avec la norme du sup (l'espace $\mathfrak{l}$∞ de Banach).
- Utiliser le fait que les tous les vecteurs en sont de norme 1, ainsi que leurs opposés et toutes les sommes finies de vecteurs de cette famille.
- Trouver une suite (ym) de vecteurs de E' convergent vers 0 pour la norme de c0 et ne convergeant pas vers 0 pour la norme de $\mathfrak{l}$1.
- Si u ∈E" considérer la suite u(en).
- Il faut donc, dans un premier temps montrer que les sommes finies $s_{n}=\sum_{k=0}^{n}\left | \eta_{k} \right |$ sont bornées.
Posons an=en si ηn≥0 et an=-en si ηn<0. Soit $v_{n}=\sum_{k=0}^{n}a_{k}$ alors tous les vn sont de norme 1 et ||u(vn)||=sn. Si u est continu tous les nombres sn sont bornés et si $s=\sum_{k=0}^{\infty }\left | \eta_{k} \right |$ on a bien ||u||≥s.
Soit maintenant x=(xn) un vecteur quelconque de c0. Nous avons vu dans cet exercice que $x=\sum_{k=0}^{\infty }x_{n}e_{n}$, nous en tirons par la continuité de u que $u(x)=\sum_{k=0}^{\infty }x_{n}\eta_{n}$ et que $|u(x)|\leq \sum_{k=0}^{\infty }|x_{n}||\eta_{n}|$ mais si ||x||≤1 on a supn|xn|≤1 et donc $|u(x)|\leq \sum_{k=0}^{\infty }|x_{n}||\eta_{n}|\leq \sum_{k=0}^{\infty }|\eta_{n}|$ qui prouve que ||u||≤s et donc finalement que ||u||=s. - Soit y2 le vecteur (1/2,1/4,1/8, ...., 1/2n, ....).
Soit y3 le vecteur (1/3,2/3×1/2,2/3×1/4, ...., (2/3)×(1/2n), ....).
.......
Soit ym le vecteur (1/m,(m-1)/2m,(m-1)/4m, ...., (m-1)/(m×2n), ....).
Alors tous les ym sont des suites décroissantes de réels positifs. Donc ||ym|| dans l'espace c0 est 1/m, mais il est clair que dans l'espace $\mathfrak{l}$1 tous les ym sont de norme 1. - u étant un élément de E", la suite vn=u(en) est nécessairement bornée et si x=(xn) est un élément de E' on a nécessairement $u(x)=\sum_{n=0 }^{\infty}v_{n}x_{n}$ et $$|u(x)|\leq \sum_{n=0 }^{\infty}|v_{n}||x_{n}|\leq \sup_{n}|v_{n}|\sum_{n=0}^{\infty }|x_{n}|$$
ce qui montre que la norme de u dans E" est au plus égale à supn|vn|. Pour Montrer que la norme de u dans E" est exactement ce nombre, soit b, on choisit un indice n tel que |vn-b|≤ε puis on calcule |u(en)| pour cet indice n particulier, et on remarque que ce nombre est inférieur à la norme de u dans E".
Exercices sur les hyperplans fermés et formes linéaires continues
- Montrer que l' application f→f(0) est une forme linéaire continue et calculer sa norme.
- Montrer que l'application $f\rightarrow \int_{0}^{1}f(x)dx$ est une forme linéaire continue et calculer sa norme.
- Comme |f(0)|≤ Supx∈[0,1]|f(x)| la norme de la forme linéaire est ≤1 mais en prenant la constante f=1 on voit que la norme est exactement 1.
- Comme $|\int_{0}^{1}f(x)dx| \leq \sup_{0\leq x\leq 1}|f(x)|$ la norme de la forme linéaire est ≤1 mais en prenant la constante f=1 on voit que la norme est exactement 1.
Soit u la forme linéaire sur E définie par u(f)=f(0).
Montrer que u n'est pas continue.
Exercices sur les espaces normés de dimension finie
Pour tout élément $P=\sum_{i=0}^{p}a_{i}X^{i}$ on pose :
$\left \| P \right \|_{1}=\sum_{i=0}^{p}\left | a_{i} \right |$
$\left \| P \right \|_{2}=\left ( \sum_{i=0}^{p}\left | a_{i}^{2} \right | \right )^{\frac{1}{2}}$
$\left \| P \right \|_{\infty }=\sup_{i}|a_{i}|$
Montrer que ce sont 3 normes sur E. Sont-elles équivalentes ?
Même question sur le sous-espace Fn de E des polynômes de degré au plus égal à n.
Alors ||Pn||∞=1 ∀ n
limn→∞ ||Pn||1=+∞
limn→∞ ||Pn||2=π/√6
Il en résulte que || ||1 n'est équivalente ni à || ||∞ ni à || ||2.
Prenant maintenant $Q_{n}=\sum_{i=0}^{n}\frac{1}{\sqrt{i+1}}X^{i}$ on voit que || ||∞ n'est pas équivalente à || ||2.
Fn étant de dimension finie n+1, les restrictions à Fn de ces trois normes sont équivalentes.
- Prouver que N est une norme sur E.
- Quelle est la boule unité de centre O=(0,0) ?
- || ||2 étant la norme euclidienne usuelle sur E, déterminer le plus petit nombre p>0 tel que N≤p|| ||2 et le plus grand entier q tel que q|| ||2≤N
- L'inégalité du triangle s'écrit :
$$\sqrt{a^{2}(x+x')^{2}+b^{2}(y+y')^{2}}\leq \sqrt{a^{2}x^{2}+b^{2}y^{2}}+\sqrt{a^{2}x'^{2}+b^{2}y'^{2}}$$
Après élévation au carré, développement et simplification par 2 elle devient :
$$a^{2}xx'+b^{2}yy'\leq \sqrt{(a^{2}x^{2}+b^{2}y^{2})(a^{2}x'^{2}+b^{2}y'^{2})}$$
Après une nouvelle élévation au carré et simplification, elle devient :
$$2xx'yy'\leq x^{2}y'^{2}+x'^{2}y^{2}$$
qui est équivalent à (xy'-yx')2≥0 - La boule unité est l'intérieur de l'ellispe d'équation
$$\frac{x^{2}}{\frac{1}{a^{2}}}+\frac{y^{2}}{\frac{1}{b^{2}}}=1$$ - L'inégalité N≤p|| ||2 équivaut à
$(a^{2}-p^{2})x^{2}+(b^{2}-p^{2})y^{2}\leq 0$ pour tous les couples de réels (x,y). Elle équivaut donc à p≥max(a,b).
De la même façon, en explicitant q|| ||2≤N il vient q≤min(a,b).
Exercices sur les espaces normés séparables
Pour toute λ∈ $\mathfrak{P}$($\mathbb{N}$) nous désignons par xλ la suite (ξn) définie par ξn=1 si n∈λ et ξn=0 si n∉λ. Alors il est clair que xλ-xμ est une suite (ξn) où ξn vaut 0 si n∈λ∩μ et soit 1, soit -1 dans le cas contraire. Donc dans tous les cas ||xλ-xμ||=1 pour λ≠μ.
Supposons maintenant que l∞ soit séparable et soit (yn) une suite dense de cet espace.
Alors pour tout λ la boule de centre xλ et de rayon 1/2 contiendrait un yn(λ). Il résulte de ce qui précède que pour λ≠μ yn(λ)≠yn(μ). La suite (yn) posséderait donc un sous ensemble non dénombrable.
